مقدمه
اعداد مختلط هنوز هم درنظر برخی با شک آمیخته با ترس همراه است. ولی درنظر ریاضیدانان امروزی این دستگاه صرفا گسترش مجموعه بنیاد سادهای از اعداد حقیقی است. همیلتون (Hamilton) ریاضیدان قرن نوزدهم گسترشی برای اعداد مختلط پیدا کرد و آن را چهارگانها نامید. ماهیت ریاضیات جدید چنان است که باید دید خود را وسیعتر کنیم و به دستگاههایی اصل موضوعی بپردازیم که بافتهای ریاضی مفیدتری را بدست دهند. مفهوم عدد چیزی جز قسمتی از این برای کلی نیست. جبر جدید یا دستگاههایی اصل موضوعی سروکار دارد که ، بطور کلی متشکل از مجموعههایی است همراه با عملهای مختلفی روی آن مجموعهها. دوتا از این دستگاهها عبارتند از حلقه و میدان. اگر بخواهیم پا را از اعداد مختلط فراتر نهیم، مسیر پربار راه چهارگانهای همیلتون نیست بلکه مسیر ساختهای جبری تقسیم یافته جبر جدید است.
تعریف
هر عدد مختلط توسط عبارت 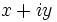 مشخص میشود که نقطهای از صفحه را مشخص میکند در هر عدد مختلط
مشخص میشود که نقطهای از صفحه را مشخص میکند در هر عدد مختلط  ا قسمت حقیقی و
ا قسمت حقیقی و 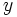 (ضریب
(ضریب 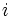 ) را قسمت موهومی عدد می نامیم. در تعریف عدد مختلط این حقیقت را میپذیریم که
) را قسمت موهومی عدد می نامیم. در تعریف عدد مختلط این حقیقت را میپذیریم که
Latex Error:
{(i)
است و به این ترتیب مشکل جذر اعداد منفی مرتفع میگردد.
دورنمای تاریخی
در دنیای مالی بدهکار و بستانکار امروزی اعداد منفی جزئی از زندگی روزمره شدهاند. جالبتر آن عرضه اعداد مختلط است. لایبنیتز میدانست که مربع هر عدد مثبت یا منفی ، عددی است مثبت. اگر 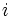 ریشه دوم منهای یک باشد. پس
ریشه دوم منهای یک باشد. پس 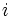 نمیتواند عددی مثبت یا منفی باشد. لایبنیتز معتقد بود که
نمیتواند عددی مثبت یا منفی باشد. لایبنیتز معتقد بود که 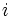 را باید عددی بسیار مرموز تلقی کرد: عددی که نه کوچکتر از صفر است و نه بزرگتر از صفر. این امر به سردرگمی بسیاری منجر شد و اعداد مختلط را با سوءظن همراه نمود. در اوایل قرن ۱۶ اشتیاق فراوانی برای حل معادلات جبری وجود داشت و از آن جمله بود پیداکردن دو عدد که مجموعشان ده و حاصلضرب آنها ۴ باشد با نمادگذاری و حل امروزی جوابی که برای
را باید عددی بسیار مرموز تلقی کرد: عددی که نه کوچکتر از صفر است و نه بزرگتر از صفر. این امر به سردرگمی بسیاری منجر شد و اعداد مختلط را با سوءظن همراه نمود. در اوایل قرن ۱۶ اشتیاق فراوانی برای حل معادلات جبری وجود داشت و از آن جمله بود پیداکردن دو عدد که مجموعشان ده و حاصلضرب آنها ۴ باشد با نمادگذاری و حل امروزی جوابی که برای  پیدا میشود عبارت است از
پیدا میشود عبارت است از
Latex Error:
{۵ \pm \sqrt{-15}}
. اویلر ریاضیدان قرن ۱۸ نماد 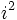 را برای
را برای 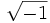 معرفی نمود.
معرفی نمود.
نحوه ساختن اعداد مختلط
فرض کنیم
Latex Error:
{\no C}
نام دیگری برای 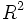 ، مجموعه زوجهای مرتب
، مجموعه زوجهای مرتب 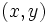 به ازای
به ازای 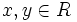 باشد، جمع و ضرب را روی
باشد، جمع و ضرب را روی
Latex Error:
{\no C}
به صورت جمع و ضرب بصورت مولفههای نظیربهنظیر خواهیم داشت به آسانی ثابت میشود که
Latex Error:
{\no C}
تحت این عملها میدانی است که 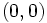 صفر آن و
صفر آن و
Latex Error:
{(۱,۰)}
یکه آن است. قرینه
Latex Error:
{(-x,-y) , (x,y)}
و اگر
Latex Error:
{(x,y) \ne (0,0)}
وارون ضربی 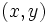 آن
آن
Latex Error:
{(\frac{x}{x
۲ + y
۲ + y
است.
تابع 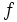 را با
را با
Latex Error:
{f(x)=(x,0)}
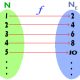
تعریف میکنیم که جمع و ضرب آن قابل تعریف است تابع 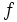 بوضوح یکبهیک است و لذا یک یکریختی میدانهاست؛ از
بوضوح یکبهیک است و لذا یک یکریختی میدانهاست؛ از  بر روی زیر میدان
بر روی زیر میدان
Latex Error:
{f(R) \mathbb \no C}
. این زیر میدان
Latex Error:
{f(R)}
چیزی جز محور حقیقی توصیف آرگان ریاضیدان فرانسوی برای عدد مختلط نیست. طبق معمول  را با توجه به یکریختی فوق بعنوان زیرمجموعه از
را با توجه به یکریختی فوق بعنوان زیرمجموعه از
Latex Error:
{\no C}
تلقی میکنیم. بدین معنی که اعداد حقیقی را بعنوان محور حقیقی صفحه مختلط را درنظر میگیریم و نماد  را به جای
را به جای
Latex Error:
{(x,0)}
بکار میبریم. 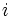 را زوج مرتب
را زوج مرتب 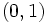 تعریف میکنیم و لذا داریم:
تعریف میکنیم و لذا داریم:
Latex Error:
{i
۲ = (۰,۱)
بنابراین با درنظر گرفتن
Latex Error:
{(-۱,۰)}
بعنوان عدد حقیقی -۱ داریم:
Latex Error:
{i
۲ = -۱}
و بطور کلی خواهیم داشت:
Latex Error:
{(x,0) + (0,1)(y,0) = (x,0) + (0,y) = (x,y)}
اگر
Latex Error:
{(y,0) , (x,0)}
را به ترتیب با 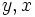 از
از  عوض کنیم، عبارت فوق بیان میکند که
عوض کنیم، عبارت فوق بیان میکند که
Latex Error:
{x+iy = (x,y)}
“عدد مختلط” 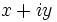 نام دیگری برای زوج مرتب
نام دیگری برای زوج مرتب 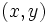 است.
است.
راه آینده
درس آنالیز اساسا مطالعه صوری حد ، مشتق و انتگرال است برپایه اصول موضوع اعداد حقیقی. ابتدا توابع
Latex Error:
{f: D \rightarrow R}
که در آن
Latex Error:
{D \mathbb R}
، درنظر گرفته میشود. سپس میپردازند به توابع
Latex Error:
{f: D \rightarrow R
با شرط
Latex Error:
{D \mathbb R
n}
.
آنالیز مختلط ، توابع مشتقپذیر
Latex Error:
{f: D \rightarrow \no C}
را که در آن
Latex Error:
{D \mathbb \no C}
مورد مطالعه قرار میدهد. در قرن اخیر هندسه بوسیله ساختهای جبری تسخیر شده، البته زبان هندسی همچنان محفوظ مانده است تا ویژگی مورد انتظار از موضوع سلب نشود. منشا توپولوژی را میتوان در مفهوم فضای متریک جستجو کرد. این فضا به بیان ساده مجموعهای است چون 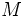 با تابعی مانند
با تابعی مانند
Latex Error:
{d: M \times M \rightarrow R}
بطوریکه
Latex Error:
{d(x,y)}
رفتاری شبیه به “تابع فاصلهای” بین 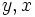 داشته باشد. که در
داشته باشد. که در
Latex Error:
{ R}




![[wpgmza id="1"]](https://hemmat.salamsch.com/hschool/wp-content/uploads/2020/12/location-marker-flat-80x80.png)